Contact info
Word
Research
Publications
Studies
Free Software
Hobbies
Articles
Photography
About me
Curriculum Vitae

High Performance Computing -course at TUCS
- My exercise resultsContents:
- Parallel Computing course - Spring 2000
- Exercise 3: 2-D heat transfer simulation
- High Performance Computing course - Fall 1999
- Exercise 1: Ping-pong test
- Exercise 2: One-dimensional finite difference calculation
- Assignment: Mandebrot set visualizer
- mpi++ - A C++ wrapper for MPICH
See also the Makefile.am for all the exercises. The Makefile contains also some examples for executing the programs.
Parallel Computing course - Spring 2000
Exercise 3: 2-D heat transfer simulation
A parallel heat transfer simulation using a 2-dimensional finite difference Gauss-Seidel successive over-relaxation (SOR) scheme.The model is a square grid of size NxN. We use a two-dimensional process grid with qxq processes (2-dimensional block decomposition, N is not necessarily evenly divisible by q). The communications are "safe".
In this example we computed the heat distribution in 150x150 points (N=150). Temperature along left, upper and right edges was 100.0 degrees, and in the lower adge and interior points 0.0 degrees. The omega parameter for SOR was 1.2, and the termination criteria was epsilon=0.001. The termination criteria was met in about 6500 iterations. This is more than it should be with this problem (about 4000), but I have no idea about the reason.
- Exercise description in Adobe Acrobat format (.pdf)
- heat.cc (main program)
- fdgrid.h - general 2D finite difference grid
- fdgrid.cc - general 2D finite difference grid
BUG: There are two problems with the mouse click checking. It seems to be possible to get mouse input for only one processor, and therefore reporting the temperature at an arbitrary point would require the one processor to know all the temperatures in the full matrix. This is not nice. The second problem is that differentiating between different mouse buttons doesn't seem to work for some reason.
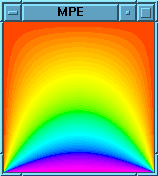
After about 100 iterations
After about 5000 iterations (practically converged).
Assignment: N-body simulation
- nbody.ps.gz - documentation
- nbody.cc - main program
- nbody.h - headers
- nbody.cfg - configuration file
High Performance Computing course - Fall 1999
Exercise 1: Ping-pong test
- Exercise description in Adobe Acrobat format (.pdf)
- Exercise answers in Adobe Acrobat format (.pdf)
- ping.cc (main program)
Exercise 2: One-dimensional finite difference calculation
Wire fragments and elements
- Exercise description (.pdf, Adobe Acrobat).
- wire.cc - main program
- wireelement.h, wireelement.cc - wire segments and elements
The entire wire is distributed as np-1 WireFragment objects, where np is the number of processors/processes. Thus, there is one fragment for each slave process.The solution is based on an object-oriented model, where the elements of the wire are autonomous objects, not just simple values in a vector. All the wire elements contained in a WireFragment inherit the superclass AnyElement. The ends of the entire wire, which are at static temperatures, are of type StaticElement, and their values do not change at any time. All other elements are of type WireElement, which determine their temperature from two neighbouring elements.
As the wire is distributed to several processors (or processes), some of the WireElements have to communicate with each other. This is implemented by the CommElement elements, which inherit the WireElement and send their temperature over the MPI interface to the CommElements in the neighbouring wire processes.
Processes
The process hierarchy is such that there is one master process, which just collects data from all the slaves, which do the actual computing. The master also tells the slaves when it is time to stop.Synchronization is somewhat strict; slave processes are synchronized by the communication between neighbouring segments. The master process is synchronized with the slaves so that after the master has received cycle reports from the slaves, it tells them whether to stop or to continue. I think that this causes a lot of speed-loss, because the children have to wait the master, and can't go on computing.
I made some tests where the master was not synchronized with the slaves, but the slaves sent their cycle reports with non-blocking messages, and then checked if a (non-blocking) termination order had arrived from the master. The problem was that, because the master was too slow in reporting (mostly plotting with Gnuplot), the children ran maybe twice too long before the master had processed their results.
Reporting
The master currently reports the results in a Gnuplot window, which is somewhat slow.The communication gaps between the wire segments are illustrated with gaps in the curve (three segments in the wire of the picture on right).
Notes
The communication is currently handled with the floating-point values represented as text strings, which really isn't very efficient.
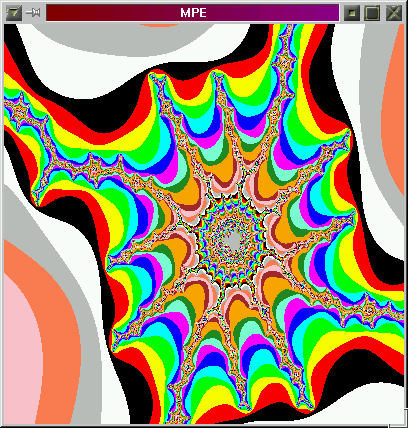
Assignment: Mandebrot set visualizer
- Assignment description (.pdf, Adobe Acrobat).
- mandel.cc - main program
- mpe++.h, mpe++.cc - C++ wrapper for the MPE graphics library
Typical output:
$ mpirun -np 4 mandel Colors=15 Time for drawing the frame: 12.8072 s Time for drawing the frame: 9.84819 s Time for drawing the frame: 23.9487 s Exiting...
Common code for all the exercises
This is a C++ wrapper to the MPI, developed for the exercises. It may not be compatible with all the exercises any longer.Note: The mpi++ wrapped has been developed under Automake&autoconf build systems and should be rather portable. However, there are some Makefile tweaks to include and link the mpich and MagiClib, so it is currently NOT very easy to compile. However, the full source is available in a package: mpi++-0.1.tar.gz (50kB). You will also need MagiClib and MPICH.
All the programs here are currently licensed under the GNU General Public License, version 2.0.